.
3.7 Nevlastní integrály
Teorii naleznete v kapitole 6.4 Multimediální encyklopedie nebo v kapitole 3.7 Breviáře
Příklad 1
Vypočítejte nevlastní integrál .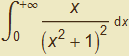
Řešení
Výpočet nevlastního integrálu s nekonečnou horní mezí, 
, zahrnuje dva kroky:
a) výpočet odpovídající primitivní funkce F(x) = ∫f(x)dx
b) dosazení do vzorce 
= 
≡ 
F(x) - F(a).
V našem případě tyto kroky nabývají konkrétní podoby:
a) Výpočet odpovídající primitivní funkce:
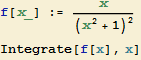
b) Dosazení do vzorce:
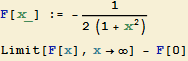
Neurčitý integrál lze rovněž vypočítat přímo:
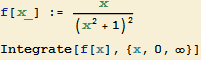
Příklad 2
Vypočítejte nevlastní integrál 
.
Řešení
Výpočet nevlastního integrálu s nekonečnou dolní mezí, 
, zahrnuje dva kroky:
a) výpočet odpovídající primitivní funkce F(x) = ∫f(x)dx,
b) dosazení do vzorce 
= 
≡ F(a) - 
F(x)
a) Výpočet primitivní funkce:
b) Dosazení do vzorce:
Neurčitý integrál lze rovněž vypočítat přímo:
Příklad 3
Vypočítejte nevlastní integrál 
.
Řešení
Vypočítejte nevlastní integrál 
.
Výpočet nevlastního integrálu s nekonečnou horní i dolní mezí, 
, zahrnuje dva kroky:
a) výpočet odpovídající primitivní funkce F(x) = ∫f(x)dx,
b) dosazení do vzorce 
= 
≡ 
F(x) - 
F(x)
a) Výpočet primitivní funkce:
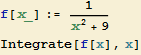
b) Dosazení do vzorce:
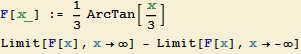
Přímý výpočet nevlastního integrálu s nekonečnou dolní i horní mezí se v programu Mathematica počítá takto:
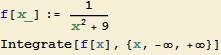
Příklad 4
Vypočítejte nevlastní integrál 
dx
Řešení
Výpočet provedeme přímo:
